OptaPlanner has several examples. In this manual we explain OptaPlanner mainly using the n queens example. So it's advisable to read at least the section about that example.
The source code of all these examples is available in the distribution zip under
examples/sources and also in git under
optaplanner/optaplanner-examples.
Table 3.1. Examples overview
| Example | Domain | Entity size | Value size | Search space | Competition? |
|---|---|---|---|---|---|
| N queens |
| <= 256 | <= 256 | <= 10^616 | Pointless |
| Cloud balancing |
| <= 2400 | <= 800 | <= 10^6967 | No |
| Traveling salesman |
| <= 980 | <= 980 | <= 10^2927 | Unrealistic |
| Manners 2009 |
| <= 144 | <= 144 | <= 10^310 | Unrealistic |
| Course timetabling |
| <= 434 | <= 25 and <= 20 | <= 10^1171 | Realistic |
| Machine reassignment |
| <= 50000 | <= 5000 | <= 10^184948 | Nearly realistic |
| Vehicle routing |
| <= 134 | <= 144 | <= 10^285 | Unrealistic |
| Vehicle routing with time windows | Extra on Vehicle Routing:
| <= ? | <= ? | <= ? | Unrealistic |
| Project job scheduling |
| <= 640 | <= ? and <= ? | <= ? | Nearly realistic |
| Hospital bed planning |
| <= 2750 | <= 471 | <= 10^6851 | Realistic |
| Exam timetabling |
| <= 1096 | <= 80 and <= 49 | <= 10^3374 | Realistic |
| Employee rostering |
| <= 752 | <= 50 | <= 10^1277 | Realistic |
| Sport scheduling |
| <= 1560 | <= 78 | <= 10^2951 | Unrealistic |
A realistic competition is an official, independent competition:
that clearly defines a real-word use case
with real-world constraints
with multiple, real-world datasets
that expects reproducible results within a specific time limit on specific hardware
that has had serious participation from the academic and/or enterprise Operations Research community
These realistic competitions provide an objective comparison of Planner with competitive software and academic research.
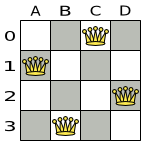
Place n queens on a n sized chessboard so no 2 queens can attach each other. The most common n queens puzzle is the 8 queens puzzle, with n = 8:

Constraints:
Use a chessboard of n columns and n rows.
Place n queens on the chessboard.
No 2 queens can attack each other. A queen can attack any other queen on the same horizontal, vertical or diagonal line.
This documentation heavily uses the 4 queens puzzle as the primary example.
A proposed solution could be:
The above solution is wrong because queens A1 and B0 can attack each
other (so can queens B0 and D0). Removing queen B0
would respect the "no 2 queens can attack each other" constraint, but would break the "place n queens"
constraint.
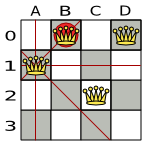
Below is a correct solution:
All the constraints have been met, so the solution is correct. Note that most n queens puzzles have multiple correct solutions. We'll focus on finding a single correct solution for a given n, not on finding the number of possible correct solutions for a given n.
4 has 4 queens with a search space of 256. 8 has 8 queens with a search space of 10^7. 16 has 16 queens with a search space of 10^19. 32 has 32 queens with a search space of 10^48. 64 has 64 queens with a search space of 10^115. 256 has 256 queens with a search space of 10^616.
The implementation of the N queens example has not been optimized because it functions as a beginner example. Nevertheless, it can easily handle 64 queens. With a few changes it has been shown to easily handle 5000 queens and more.
Use a good domain model: it will be easier to understand and solve your planning problem. This is the domain model for the n queens example:
public class Column {
private int index;
// ... getters and setters
}
public class Row {
private int index;
// ... getters and setters
}
public class Queen {
private Column column;
private Row row;
public int getAscendingDiagonalIndex() {...}
public int getDescendingDiagonalIndex() {...}
// ... getters and setters
}
A Queen instance has a Column (for example: 0 is column A, 1 is
column B, ...) and a Row (its row, for example: 0 is row 0, 1 is row 1, ...). Based on the
column and the row, the ascending diagonal line as well as the descending diagonal line can be calculated. The
column and row indexes start from the upper left corner of the chessboard.
public class NQueens implements Solution<SimpleScore> {
private int n;
private List<Column> columnList;
private List<Row> rowList;
private List<Queen> queenList;
private SimpleScore score;
// ... getters and setters
}
A single NQueens instance contains a list of all Queen instances. It
is the Solution implementation which will be supplied to, solved by and retrieved from the
Solver. Notice that in the 4 queens example, NQueens's getN() method will always return
4.
Table 3.2. A solution for 4 queens shown in the domain model
| A solution | Queen | columnIndex | rowIndex | ascendingDiagonalIndex (columnIndex + rowIndex) | descendingDiagonalIndex (columnIndex - rowIndex) |
|---|---|---|---|---|---|
 | A1 | 0 | 1 | 1 (**) | -1 |
| B0 | 1 | 0 (*) | 1 (**) | 1 | |
| C2 | 2 | 2 | 4 | 0 | |
| D0 | 3 | 0 (*) | 3 | 3 |
When 2 queens share the same column, row or diagonal line, such as (*) and (**), they can attack each other.
This example is explained in a tutorial.
Given a list of cities, find the shortest tour for a salesman that visits each city exactly once.
The problem is defined by Wikipedia. It is one of the most intensively studied problems in computational mathematics. Yet, in the real world, it's often only part of a planning problem, along with other constraints, such as employee shift rostering constraints.
In Manners 2009, miss Manners is throwing a party again.
This time she invited 144 guests and prepared 12 round tables with 12 seats each.
Every guest should sit next to someone (left and right) of the opposite gender.
And that neighbour should have at least one hobby in common with the guest.
Also, this time there should be 2 politicians, 2 doctors, 2 socialites, 2 sports stars, 2 teachers and 2 programmers at each table.
And the 2 politicians, 2 doctors, 2 sports stars and 2 programmers shouldn't be the same kind.
Drools Expert also has the normal miss Manners examples (which is much smaller) and employs a brute force heuristic to solve it. OptaPlanner's implementation is far more scalable because it uses heuristics to find the best solution and Drools Expert to calculate the score of each solution.
Schedule each lecture into a timeslot and into a room.
Hard constraints:
Teacher conflict: A teacher must not have 2 lectures in the same period.
Curriculum conflict: A curriculum must not have 2 lectures in the same period.
Room occupancy: 2 lectures must not be in the same room in the same period.
Unavailable period (specified per dataset): A specific lecture must not be assigned to a specific period.
Soft constraints:
Room capacity: A room's capacity should not be less than the number of students in its lecture.
Minimum working days: Lectures of the same course should be spread into a minimum number of days.
Curriculum compactness: Lectures belonging to the same curriculum should be adjacent to each other (so in consecutive periods).
Room stability: Lectures of the same course should be assigned the same room.
The problem is defined by the International Timetabling Competition 2007 track 3.
comp01 has 24 teachers, 14 curricula, 30 courses, 160 lectures, 30 periods, 6 rooms and 53 unavailable period constraints with a search space of 10^360. comp02 has 71 teachers, 70 curricula, 82 courses, 283 lectures, 25 periods, 16 rooms and 513 unavailable period constraints with a search space of 10^736. comp03 has 61 teachers, 68 curricula, 72 courses, 251 lectures, 25 periods, 16 rooms and 382 unavailable period constraints with a search space of 10^653. comp04 has 70 teachers, 57 curricula, 79 courses, 286 lectures, 25 periods, 18 rooms and 396 unavailable period constraints with a search space of 10^758. comp05 has 47 teachers, 139 curricula, 54 courses, 152 lectures, 36 periods, 9 rooms and 771 unavailable period constraints with a search space of 10^381. comp06 has 87 teachers, 70 curricula, 108 courses, 361 lectures, 25 periods, 18 rooms and 632 unavailable period constraints with a search space of 10^957. comp07 has 99 teachers, 77 curricula, 131 courses, 434 lectures, 25 periods, 20 rooms and 667 unavailable period constraints with a search space of 10^1171. comp08 has 76 teachers, 61 curricula, 86 courses, 324 lectures, 25 periods, 18 rooms and 478 unavailable period constraints with a search space of 10^859. comp09 has 68 teachers, 75 curricula, 76 courses, 279 lectures, 25 periods, 18 rooms and 405 unavailable period constraints with a search space of 10^740. comp10 has 88 teachers, 67 curricula, 115 courses, 370 lectures, 25 periods, 18 rooms and 694 unavailable period constraints with a search space of 10^981. comp11 has 24 teachers, 13 curricula, 30 courses, 162 lectures, 45 periods, 5 rooms and 94 unavailable period constraints with a search space of 10^381. comp12 has 74 teachers, 150 curricula, 88 courses, 218 lectures, 36 periods, 11 rooms and 1368 unavailable period constraints with a search space of 10^566. comp13 has 77 teachers, 66 curricula, 82 courses, 308 lectures, 25 periods, 19 rooms and 468 unavailable period constraints with a search space of 10^824. comp14 has 68 teachers, 60 curricula, 85 courses, 275 lectures, 25 periods, 17 rooms and 486 unavailable period constraints with a search space of 10^722.
Assign each process to a machine. All processes already have an original (unoptimized) assignment. Each process requires an amount of each resource (such as CPU, RAM, ...). This is more complex version of the Cloud Balancing example.
Hard constraints:
Maximum capacity: The maximum capacity for each resource for each machine must not be exceeded.
Conflict: Processes of the same service must run on distinct machines.
Spread: Processes of the same service must be spread across locations.
Dependency: The processes of a service depending on another service must run in the neighborhood of a process of the other service.
Transient usage: Some resources are transient and count towards the maximum capacity of both the original machine as the newly assigned machine.
Soft constraints:
Load: The safety capacity for each resource for each machine should not be exceeded.
Balance: Leave room for future assignments by balancing the available resources on each machine.
Process move cost: A process has a move cost.
Service move cost: A service has a move cost.
Machine move cost: Moving a process from machine A to machine B has another A-B specific move cost.
The problem is defined by the Google ROADEF/EURO Challenge 2012.
model_a1_1 has 2 resources, 1 neighborhoods, 4 locations, 4 machines, 79 services, 100 processes and 1 balancePenalties with a search space of 10^60. model_a1_2 has 4 resources, 2 neighborhoods, 4 locations, 100 machines, 980 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a1_3 has 3 resources, 5 neighborhoods, 25 locations, 100 machines, 216 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a1_4 has 3 resources, 50 neighborhoods, 50 locations, 50 machines, 142 services, 1000 processes and 1 balancePenalties with a search space of 10^1698. model_a1_5 has 4 resources, 2 neighborhoods, 4 locations, 12 machines, 981 services, 1000 processes and 1 balancePenalties with a search space of 10^1079. model_a2_1 has 3 resources, 1 neighborhoods, 1 locations, 100 machines, 1000 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_2 has 12 resources, 5 neighborhoods, 25 locations, 100 machines, 170 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_3 has 12 resources, 5 neighborhoods, 25 locations, 100 machines, 129 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_4 has 12 resources, 5 neighborhoods, 25 locations, 50 machines, 180 services, 1000 processes and 1 balancePenalties with a search space of 10^1698. model_a2_5 has 12 resources, 5 neighborhoods, 25 locations, 50 machines, 153 services, 1000 processes and 0 balancePenalties with a search space of 10^1698. model_b_1 has 12 resources, 5 neighborhoods, 10 locations, 100 machines, 2512 services, 5000 processes and 0 balancePenalties with a search space of 10^10000. model_b_2 has 12 resources, 5 neighborhoods, 10 locations, 100 machines, 2462 services, 5000 processes and 1 balancePenalties with a search space of 10^10000. model_b_3 has 6 resources, 5 neighborhoods, 10 locations, 100 machines, 15025 services, 20000 processes and 0 balancePenalties with a search space of 10^40000. model_b_4 has 6 resources, 5 neighborhoods, 50 locations, 500 machines, 1732 services, 20000 processes and 1 balancePenalties with a search space of 10^53979. model_b_5 has 6 resources, 5 neighborhoods, 10 locations, 100 machines, 35082 services, 40000 processes and 0 balancePenalties with a search space of 10^80000. model_b_6 has 6 resources, 5 neighborhoods, 50 locations, 200 machines, 14680 services, 40000 processes and 1 balancePenalties with a search space of 10^92041. model_b_7 has 6 resources, 5 neighborhoods, 50 locations, 4000 machines, 15050 services, 40000 processes and 1 balancePenalties with a search space of 10^144082. model_b_8 has 3 resources, 5 neighborhoods, 10 locations, 100 machines, 45030 services, 50000 processes and 0 balancePenalties with a search space of 10^100000. model_b_9 has 3 resources, 5 neighborhoods, 100 locations, 1000 machines, 4609 services, 50000 processes and 1 balancePenalties with a search space of 10^150000. model_b_10 has 3 resources, 5 neighborhoods, 100 locations, 5000 machines, 4896 services, 50000 processes and 1 balancePenalties with a search space of 10^184948.
Using a fleet of vehicles, pick up the objects of each customer and bring them to the depot. Each vehicle can service multiple customers, but it has a limited capacity.

The capacitated vehicle routing problem (CRVP) is defined by the VRP web.
A-n32-k5 has 1 depots, 5 vehicles and 31 customers with a search space of 10^46. A-n33-k5 has 1 depots, 5 vehicles and 32 customers with a search space of 10^48. A-n33-k6 has 1 depots, 6 vehicles and 32 customers with a search space of 10^48. A-n34-k5 has 1 depots, 5 vehicles and 33 customers with a search space of 10^50. A-n36-k5 has 1 depots, 5 vehicles and 35 customers with a search space of 10^54. A-n37-k5 has 1 depots, 5 vehicles and 36 customers with a search space of 10^56. A-n37-k6 has 1 depots, 6 vehicles and 36 customers with a search space of 10^56. A-n38-k5 has 1 depots, 5 vehicles and 37 customers with a search space of 10^58. A-n39-k5 has 1 depots, 5 vehicles and 38 customers with a search space of 10^60. A-n39-k6 has 1 depots, 6 vehicles and 38 customers with a search space of 10^60. A-n44-k7 has 1 depots, 7 vehicles and 43 customers with a search space of 10^70. A-n45-k6 has 1 depots, 6 vehicles and 44 customers with a search space of 10^72. A-n45-k7 has 1 depots, 7 vehicles and 44 customers with a search space of 10^72. A-n46-k7 has 1 depots, 7 vehicles and 45 customers with a search space of 10^74. A-n48-k7 has 1 depots, 7 vehicles and 47 customers with a search space of 10^78. A-n53-k7 has 1 depots, 7 vehicles and 52 customers with a search space of 10^89. A-n54-k7 has 1 depots, 7 vehicles and 53 customers with a search space of 10^91. A-n55-k9 has 1 depots, 9 vehicles and 54 customers with a search space of 10^93. A-n60-k9 has 1 depots, 9 vehicles and 59 customers with a search space of 10^104. A-n61-k9 has 1 depots, 9 vehicles and 60 customers with a search space of 10^106. A-n62-k8 has 1 depots, 8 vehicles and 61 customers with a search space of 10^108. A-n63-k10 has 1 depots, 10 vehicles and 62 customers with a search space of 10^111. A-n63-k9 has 1 depots, 9 vehicles and 62 customers with a search space of 10^111. A-n64-k9 has 1 depots, 9 vehicles and 63 customers with a search space of 10^113. A-n65-k9 has 1 depots, 9 vehicles and 64 customers with a search space of 10^115. A-n69-k9 has 1 depots, 9 vehicles and 68 customers with a search space of 10^124. A-n80-k10 has 1 depots, 10 vehicles and 79 customers with a search space of 10^149. F-n135-k7 has 1 depots, 7 vehicles and 134 customers with a search space of 10^285. F-n45-k4 has 1 depots, 4 vehicles and 44 customers with a search space of 10^72. F-n72-k4 has 1 depots, 4 vehicles and 71 customers with a search space of 10^131.
Schedule all jobs in time and execution mode to minimize project delays. Each job is part of a project. A job can be executed in different ways: each way is an execution mode that implies a different duration but also different resource usages. This is a form of flexible job shop scheduling.
Hard constraints:
Job precedence: a job can only start when all its predecessor jobs are finished.
Resource capacity: do not use more resources then available.
Resources are local (shared between jobs of the same project) or global (shared between all jobs)
Resource are renewable (capacity available per day) or nonrenewable (capacity available for all days)
Medium constraints:
Total project delay: minimize the duration (makespan) of each project.
Soft constraints:
Total makespan: minimize the duration of the whole multi-project schedule.
The problem is defined by the MISTA 2013 challenge.
Schedule A-1 has 2 projects, 24 jobs, 64 execution modes, 7 resources and 150 resource requirements. Schedule A-2 has 2 projects, 44 jobs, 124 execution modes, 7 resources and 420 resource requirements. Schedule A-3 has 2 projects, 64 jobs, 184 execution modes, 7 resources and 630 resource requirements. Schedule A-4 has 5 projects, 60 jobs, 160 execution modes, 16 resources and 390 resource requirements. Schedule A-5 has 5 projects, 110 jobs, 310 execution modes, 16 resources and 900 resource requirements. Schedule A-6 has 5 projects, 160 jobs, 460 execution modes, 16 resources and 1440 resource requirements. Schedule A-7 has 10 projects, 120 jobs, 320 execution modes, 22 resources and 900 resource requirements. Schedule A-8 has 10 projects, 220 jobs, 620 execution modes, 22 resources and 1860 resource requirements. Schedule A-9 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 2880 resource requirements. Schedule A-10 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 2970 resource requirements. Schedule B-1 has 10 projects, 120 jobs, 320 execution modes, 31 resources and 900 resource requirements. Schedule B-2 has 10 projects, 220 jobs, 620 execution modes, 22 resources and 1740 resource requirements. Schedule B-3 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 3060 resource requirements. Schedule B-4 has 15 projects, 180 jobs, 480 execution modes, 46 resources and 1530 resource requirements. Schedule B-5 has 15 projects, 330 jobs, 930 execution modes, 46 resources and 2760 resource requirements. Schedule B-6 has 15 projects, 480 jobs, 1380 execution modes, 46 resources and 4500 resource requirements. Schedule B-7 has 20 projects, 240 jobs, 640 execution modes, 61 resources and 1710 resource requirements. Schedule B-8 has 20 projects, 440 jobs, 1240 execution modes, 42 resources and 3180 resource requirements. Schedule B-9 has 20 projects, 640 jobs, 1840 execution modes, 61 resources and 5940 resource requirements. Schedule B-10 has 20 projects, 460 jobs, 1300 execution modes, 42 resources and 4260 resource requirements.
Assign each patient (that will come to the hospital) into a bed for each night that the patient will stay in the hospital. Each bed belongs to a room and each room belongs to a department. The arrival and departure dates of the patients is fixed: only a bed needs to be assigned for each night.

Hard constraints:
2 patients must not be assigned to the same bed in the same night.
A room can have a gender limitation: only females, only males, the same gender in the same night or no gender limitation at all.
A department can have a minimum or maximum age.
A patient can require a room with specific equipment(s).
Soft constraints:
A patient can prefer a maximum room size, for example if he/she want a single room.
A patient is best assigned to a department that specializes in his/her problem.
A patient is best assigned to a room that specializes in his/her problem.
A patient can prefer a room with specific equipment(s).
The problem is defined on this webpage and the test data comes from real world hospitals.
testdata01 has 4 specialisms, 2 equipments, 4 departments, 98 rooms, 286 beds, 14 nights, 652 patients and 652 admissions with a search space of 10^1601. testdata02 has 6 specialisms, 2 equipments, 6 departments, 151 rooms, 465 beds, 14 nights, 755 patients and 755 admissions with a search space of 10^2013. testdata03 has 5 specialisms, 2 equipments, 5 departments, 131 rooms, 395 beds, 14 nights, 708 patients and 708 admissions with a search space of 10^1838. testdata04 has 6 specialisms, 2 equipments, 6 departments, 155 rooms, 471 beds, 14 nights, 746 patients and 746 admissions with a search space of 10^1994. testdata05 has 4 specialisms, 2 equipments, 4 departments, 102 rooms, 325 beds, 14 nights, 587 patients and 587 admissions with a search space of 10^1474. testdata06 has 4 specialisms, 2 equipments, 4 departments, 104 rooms, 313 beds, 14 nights, 685 patients and 685 admissions with a search space of 10^1709. testdata07 has 6 specialisms, 4 equipments, 6 departments, 162 rooms, 472 beds, 14 nights, 519 patients and 519 admissions with a search space of 10^1387. testdata08 has 6 specialisms, 4 equipments, 6 departments, 148 rooms, 441 beds, 21 nights, 895 patients and 895 admissions with a search space of 10^2366. testdata09 has 4 specialisms, 4 equipments, 4 departments, 105 rooms, 310 beds, 28 nights, 1400 patients and 1400 admissions with a search space of 10^3487. testdata10 has 4 specialisms, 4 equipments, 4 departments, 104 rooms, 308 beds, 56 nights, 1575 patients and 1575 admissions with a search space of 10^3919. testdata11 has 4 specialisms, 4 equipments, 4 departments, 107 rooms, 318 beds, 91 nights, 2514 patients and 2514 admissions with a search space of 10^6291. testdata12 has 4 specialisms, 4 equipments, 4 departments, 105 rooms, 310 beds, 84 nights, 2750 patients and 2750 admissions with a search space of 10^6851. testdata13 has 5 specialisms, 4 equipments, 5 departments, 125 rooms, 368 beds, 28 nights, 907 patients and 1109 admissions with a search space of 10^2845.
Schedule each exam into a period and into a room. Multiple exams can share the same room during the same period.

Hard constraints:
Exam conflict: 2 exams that share students must not occur in the same period.
Room capacity: A room's seating capacity must suffice at all times.
Period duration: A period's duration must suffice for all of its exams.
Period related hard constraints (specified per dataset):
Coincidence: 2 specified exams must use the same period (but possibly another room).
Exclusion: 2 specified exams must not use the same period.
After: A specified exam must occur in a period after another specified exam's period.
Room related hard constraints (specified per dataset):
Exclusive: 1 specified exam should not have to share its room with any other exam.
Soft constraints (each of which has a parametrized penalty):
The same student should not have 2 exams in a row.
The same student should not have 2 exams on the same day.
Period spread: 2 exams that share students should be a number of periods apart.
Mixed durations: 2 exams that share a room should not have different durations.
Front load: Large exams should be scheduled earlier in the schedule.
Period penalty (specified per dataset): Some periods have a penalty when used.
Room penalty (specified per dataset): Some rooms have a penalty when used.
It uses large test data sets of real-life universities.
The problem is defined by the International Timetabling Competition 2007 track 1. Geoffrey De Smet finished 4th in that competition with a very early version of OptaPlanner. Many improvements have been made since then.
exam_comp_set1 has 7883 students, 607 exams, 54 periods, 7 rooms, 12 period constraints and 0 room constraints with a search space of 10^1564. exam_comp_set2 has 12484 students, 870 exams, 40 periods, 49 rooms, 12 period constraints and 2 room constraints with a search space of 10^2864. exam_comp_set3 has 16365 students, 934 exams, 36 periods, 48 rooms, 168 period constraints and 15 room constraints with a search space of 10^3023. exam_comp_set4 has 4421 students, 273 exams, 21 periods, 1 rooms, 40 period constraints and 0 room constraints with a search space of 10^360. exam_comp_set5 has 8719 students, 1018 exams, 42 periods, 3 rooms, 27 period constraints and 0 room constraints with a search space of 10^2138. exam_comp_set6 has 7909 students, 242 exams, 16 periods, 8 rooms, 22 period constraints and 0 room constraints with a search space of 10^509. exam_comp_set7 has 13795 students, 1096 exams, 80 periods, 15 rooms, 28 period constraints and 0 room constraints with a search space of 10^3374. exam_comp_set8 has 7718 students, 598 exams, 80 periods, 8 rooms, 20 period constraints and 1 room constraints with a search space of 10^1678.
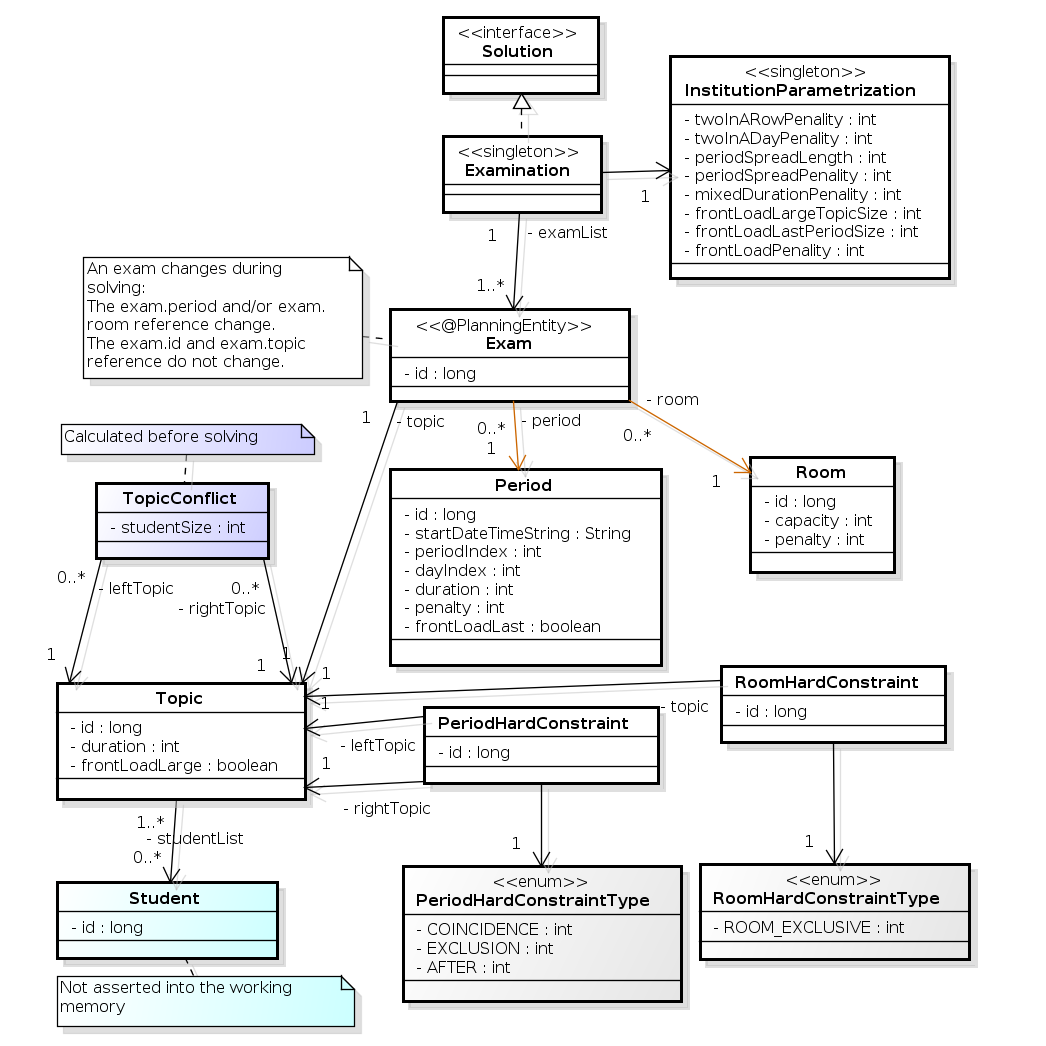
Below you can see the main examination domain classes:
Notice that we've split up the exam concept into an Exam class and a
Topic class. The Exam instances change during solving (this is the
planning entity class), when their period or room property changes. The Topic,
Period and Room instances never change during solving (these are problem
facts, just like some other classes).
For each shift, assign a nurse to work that shift.



The problem is defined by the International Nurse Rostering Competition 2010.
There are 3 dataset types:
sprint: must be solved in seconds.
medium: must be solved in minutes.
long: must be solved in hours.
toy1 has 1 skills, 3 shiftTypes, 2 patterns, 1 contracts, 6 employees, 7 shiftDates, 35 shiftAssignments and 0 requests with a search space of 10^27. toy2 has 1 skills, 3 shiftTypes, 3 patterns, 2 contracts, 20 employees, 28 shiftDates, 180 shiftAssignments and 140 requests with a search space of 10^234. sprint01 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint02 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint03 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint04 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint05 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint06 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint07 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint08 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint09 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint10 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint01 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint02 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint03 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late01 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late02 has 1 skills, 3 shiftTypes, 4 patterns, 3 contracts, 10 employees, 28 shiftDates, 144 shiftAssignments and 139 requests with a search space of 10^144. sprint_late03 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 160 shiftAssignments and 150 requests with a search space of 10^160. sprint_late04 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 160 shiftAssignments and 150 requests with a search space of 10^160. sprint_late05 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late06 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late07 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late08 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 0 requests with a search space of 10^152. sprint_late09 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 0 requests with a search space of 10^152. sprint_late10 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. medium01 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium02 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium03 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium04 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium05 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium_hint01 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_hint02 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_hint03 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late01 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 424 shiftAssignments and 390 requests with a search space of 10^626. medium_late02 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late03 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late04 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 416 shiftAssignments and 390 requests with a search space of 10^614. medium_late05 has 2 skills, 5 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 452 shiftAssignments and 390 requests with a search space of 10^667. long01 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long02 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long03 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long04 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long05 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long_hint01 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_hint02 has 2 skills, 5 shiftTypes, 7 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_hint03 has 2 skills, 5 shiftTypes, 7 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_late01 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late02 has 2 skills, 5 shiftTypes, 9 patterns, 4 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late03 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late04 has 2 skills, 5 shiftTypes, 9 patterns, 4 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late05 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257.
Schedule matches between n teams.

Hard constraints:
Each team plays twice against every other team: once home and once away.
Each team has exactly 1 match on each timeslot.
No team must have more than 3 consecutive home or 3 consecutive away matches.
No repeaters: no 2 consecutive matches of the same 2 opposing teams.
Soft constraints:
Minimize the total distance traveled by all teams.
The problem is defined on Michael Trick's website (which contains the world records too).
1-nl04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 1-nl06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 1-nl08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 1-nl10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 1-nl12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 1-nl14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 1-nl16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 2-bra24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 3-nfl16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 3-nfl18 has 34 days, 18 teams and 306 matches with a search space of 10^468. 3-nfl20 has 38 days, 20 teams and 380 matches with a search space of 10^600. 3-nfl22 has 42 days, 22 teams and 462 matches with a search space of 10^749. 3-nfl24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 3-nfl26 has 50 days, 26 teams and 650 matches with a search space of 10^1104. 3-nfl28 has 54 days, 28 teams and 756 matches with a search space of 10^1309. 3-nfl30 has 58 days, 30 teams and 870 matches with a search space of 10^1534. 3-nfl32 has 62 days, 32 teams and 992 matches with a search space of 10^1778. 4-super04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 4-super06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 4-super08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 4-super10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 4-super12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 4-super14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 5-galaxy04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 5-galaxy06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 5-galaxy08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 5-galaxy10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 5-galaxy12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 5-galaxy14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 5-galaxy16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 5-galaxy18 has 34 days, 18 teams and 306 matches with a search space of 10^468. 5-galaxy20 has 38 days, 20 teams and 380 matches with a search space of 10^600. 5-galaxy22 has 42 days, 22 teams and 462 matches with a search space of 10^749. 5-galaxy24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 5-galaxy26 has 50 days, 26 teams and 650 matches with a search space of 10^1104. 5-galaxy28 has 54 days, 28 teams and 756 matches with a search space of 10^1309. 5-galaxy30 has 58 days, 30 teams and 870 matches with a search space of 10^1534. 5-galaxy32 has 62 days, 32 teams and 992 matches with a search space of 10^1778. 5-galaxy34 has 66 days, 34 teams and 1122 matches with a search space of 10^2041. 5-galaxy36 has 70 days, 36 teams and 1260 matches with a search space of 10^2324. 5-galaxy38 has 74 days, 38 teams and 1406 matches with a search space of 10^2628. 5-galaxy40 has 78 days, 40 teams and 1560 matches with a search space of 10^2951.