JBoss.orgCommunity Documentation

Chapter 4. Planner configuration

4.1. Overview
4.2. Solver configuration
4.2.1. Solver configuration by XML
4.2.2. Solver configuration by Java API
4.3. Model a planning problem
4.3.1. Is this class a problem fact or planning entity?
4.3.2. Problem fact
4.3.3. Planning entity
4.3.4. Planning variable
4.3.5. Planning value and planning value range
4.3.6. Shadow variable
4.3.7. Planning problem and planning solution
4.4. Use the Solver
4.4.1. The Solver interface
4.4.2. Solving a problem
4.4.3. Environment mode: Are there bugs in my code?
4.4.4. Logging level: What is the Solver doing?
4.4.5. Random number generator

4.1. Overview

Solving a planning problem with Planner consists out of 5 steps:

  1. Model your planning problem as a class that implements the interface Solution, for example the class NQueens.

  2. Configure a Solver, for example a First Fit and Tabu Search solver for any NQueens instance.

  3. Load a problem data set from your data layer, for example a 4 Queens instance. That is the planning problem.

  4. Solve it with Solver.solve(planningProblem).

  5. Get the best solution found by the Solver with Solver.getBestSolution().

4.2. Solver configuration

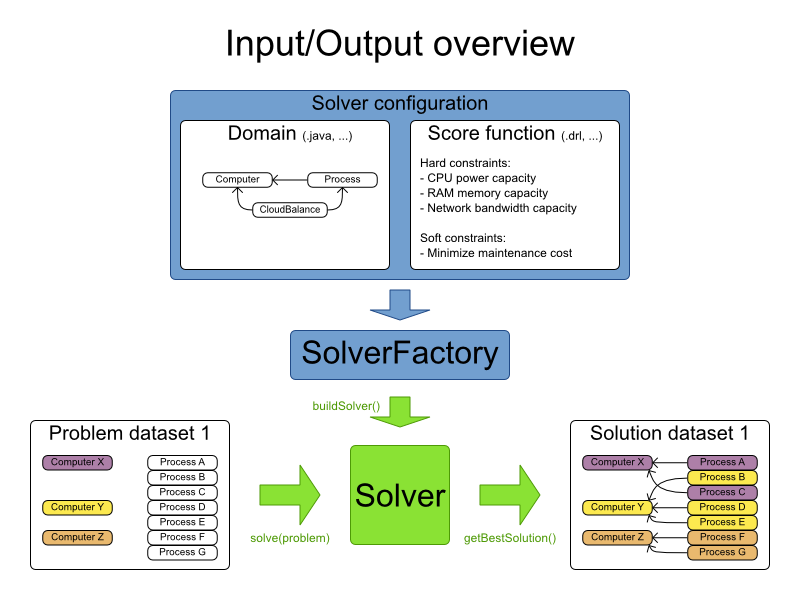
Build a Solver instance with the SolverFactory. Configure it with a solver configuration XML file, provided as a classpath resource (as definied by ClassLoader.getResource()):

       SolverFactory solverFactory = SolverFactory.createFromXmlResource(
               "org/optaplanner/examples/nqueens/solver/nqueensSolverConfig.xml");
       Solver solver = solverFactory.buildSolver();

In a typical project (following the Maven directory structure), that solverConfig XML file would be located at $PROJECT_DIR/src/main/resources/org/optaplanner/examples/nqueens/solver/nqueensSolverConfig.xml. On some environments (OSGi, JBoss modules, ...), classpath resources in your jars might not be available in by default to the classes in optaplanner's jars.

Alternatively, a SolverFactory can be created from a File, an InputStream or a Reader with methods such as SolverFactory.createFromXmlFile(). However, for portability reasons, a classpath resource is recommended.

A solver configuration file looks like this:

<?xml version="1.0" encoding="UTF-8"?>
<solver>
  <!-- Define the model -->
  <solutionClass>org.optaplanner.examples.nqueens.domain.NQueens</solutionClass>
  <entityClass>org.optaplanner.examples.nqueens.domain.Queen</entityClass>

  <!-- Define the score function -->
  <scoreDirectorFactory>
    <scoreDefinitionType>SIMPLE</scoreDefinitionType>
    <scoreDrl>org/optaplanner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>
  </scoreDirectorFactory>

  <!-- Configure the optimization algorithm(s) -->
  <termination>
    ...
  </termination>
  <constructionHeuristic>
    ...
  </constructionHeuristic>
  <localSearch>
    ...
  </localSearch>
</solver>

Notice the 3 parts in it:

  • Define the model

  • Define the score function

  • Configure the optimization algorithm(s)

These various parts of a configuration are explained further in this manual.

Planner makes it relatively easy to switch optimization algorithm(s) just by changing the configuration. There's even a Benchmarker utility which allows you to play out different configurations against each other and report the most appropriate configuration for your use case.

A solver configuration can also be configured with the SolverConfig API. This especially useful to change some values dynamically at runtime, for example to change the running time based on user input, before building the Solver:

        SolverFactory solverFactory = SolverFactory.createFromXmlResource(
                "org/optaplanner/examples/nqueens/solver/nqueensSolverConfig.xml");

        SolverConfig solverConfig = solverFactory.getSolverConfig();
        TerminationConfig terminationConfig = solverConfig.getTerminationConfig();
        terminationConfig.setMinutesSpentLimit(userInput);

        Solver solver = solverFactory.buildSolver();

Every element in the solver configuration XML is available as a *Config class or a property on a *Config class in the package namespace org.optaplanner.core.config. These *Config classes are the Java representation of the XML format and they also provide the user-friendly way to assemble the runtime components (of the package namespace org.optaplanner.core.impl) into an efficient Solver.

4.3. Model a planning problem

Look at a dataset of your planning problem. You'll recognize domain classes in there, each of which can be categorized as one of these:

Ask yourself: What class changes during planning? Which class has variables that I want the Solver to change for me? That class is a planning entity. Most use cases have only 1 planning entity class. Most use cases also have only 1 planning variable per planning entity class.

Note

In real-time planning, even thought the problem itself changes, problem facts don't really change during planning, instead they change between planning (because the Solver temporarily stops to apply the problem fact changes).

A good model can greatly improve the success of your planning implementation. Follow these guidelines to design a good model:

  • In a many to one relationship, it's normally the many side that is the planning entity class. The property referencing the other side is then the planning variable. For example in employee rostering: the planning entity class is ShiftAssignment, not Employee, and the planning variable is ShiftAssignment.getEmployee() because 1 Employee has multiple ShiftAssignments but 1 ShiftAssignment has only 1 Employee.

  • A planning entity class should have at least 1 problem property. A planning entity class with only planning variables can normally be simplified by converting 1 of those planning variables into a problem property. That heavily decreases the search space size. For example in employee rostering: the ShiftAssignment's getShift() is a problem property and the getEmployee() is a planning variable. If both were a planning variable, solving it would be far less efficient.

    • A surrogate ID does not suffice as that at least 1 problem property. It needs to be understandable by the business. A business key does suffice. This prevents an unassigned entity from being nameless (unidentifiable by the business).

    • This way, there is no need to add a hard constraint to assure that 2 planning entities are different: they are already different due to their problem properties.

    • In some cases, multiple planning entities have the same problem property. In such cases, it can be useful to create an extra problem property to distinguish them. For example in employee rostering: ShiftAssignment has besides the problem property Shift also the problem property indexInShift.

  • The number of planning entities is recommended to be fixed during planning. When in doubt which property should be a planning variable and which should be a problem property, choose it so the number of planning entities is fixed. For example in employee rostering: if the planning entity class would have been EmployeeAssignment with a problem property getEmployee() and a planning variable getShift(), than it's impossible to accurately predict how many EmployeeAssignment instances to make per Employee.

For inspiration, take a look at how the examples modeled their domain:

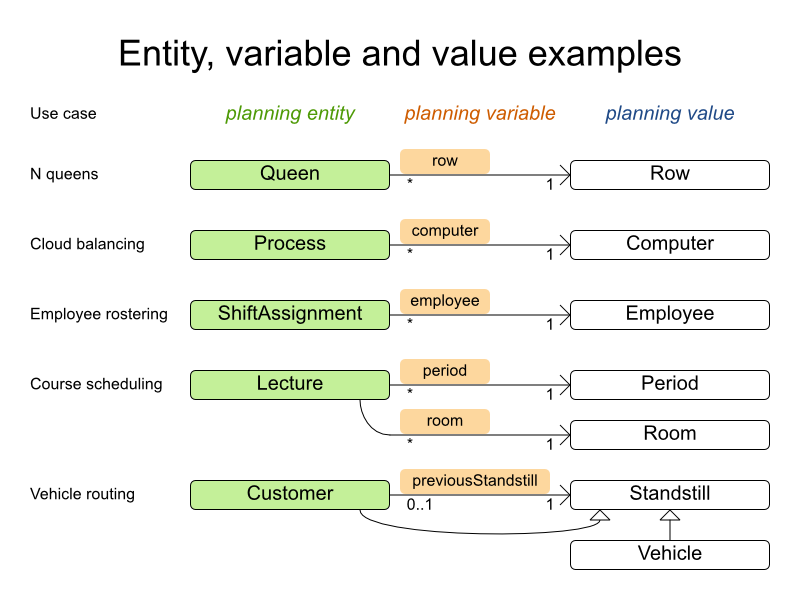
Note

Vehicle routing is special, because it uses a chained planning variable.

In Planner all problems facts and planning entities are plain old JavaBeans (POJO's). You can load them from a database, an XML file, a data repository, a noSQL cloud, ... (see Integration): Planner doesn't care.

A problem fact is any JavaBean (POJO) with getters that does not change during planning. Implementing the interface Serializable is recommended (but not required). For example in n queens, the columns and rows are problem facts:

public class Column implements Serializable {

    private int index;

    // ... getters
}
public class Row implements Serializable {

    private int index;

    // ... getters
}

A problem fact can reference other problem facts of course:

public class Course implements Serializable {

    private String code;

    private Teacher teacher; // Other problem fact
    private int lectureSize;
    private int minWorkingDaySize;

    private List<Curriculum> curriculumList; // Other problem facts
    private int studentSize;

    // ... getters
}

A problem fact class does not require any Planner specific code. For example, you can reuse your domain classes, which might have JPA annotations.

Note

Generally, better designed domain classes lead to simpler and more efficient score constraints. Therefore, when dealing with a messy legacy system, it can sometimes be worth it to convert the messy domain set into a planner specific POJO set first. For example: if your domain model has 2 Teacher instances for the same teacher that teaches at 2 different departments, it's hard to write a correct score constraint that constrains a teacher's spare time.

Alternatively, you can sometimes also introduce a cached problem fact to enrich the domain model for planning only.

A planning entity is a JavaBean (POJO) that changes during solving, for example a Queen that changes to another row. A planning problem has multiple planning entities, for example for a single n queens problem, each Queen is a planning entity. But there's usually only 1 planning entity class, for example the Queen class.

A planning entity class needs to be annotated with the @PlanningEntity annotation.

Each planning entity class has 1 or more planning variables. It usually also has 1 or more defining properties. For example in n queens, a Queen is defined by its Column and has a planning variable Row. This means that a Queen's column never changes during solving, while its row does change.

@PlanningEntity
public class Queen {

    private Column column;

    // Planning variables: changes during planning, between score calculations.
    private Row row;

    // ... getters and setters
}

A planning entity class can have multiple planning variables. For example, a Lecture is defined by its Course and its index in that course (because 1 course has multiple lectures). Each Lecture needs to be scheduled into a Period and a Room so it has 2 planning variables (period and room). For example: the course Mathematics has 8 lectures per week, of which the first lecture is Monday morning at 08:00 in room 212.

@PlanningEntity
public class Lecture {

    private Course course;
    private int lectureIndexInCourse;

    // Planning variables: changes during planning, between score calculations.
    private Period period;
    private Room room;

    // ...
}

The solver configuration also needs to be made aware of each planning entity class:

<solver>
  ...
  <entityClass>org.optaplanner.examples.nqueens.domain.Queen</entityClass>
  ...
</solver>

Some uses cases have multiple planning entity classes. For example: route freight and trains into railway network arcs, where each freight can use multiple trains over its journey and each train can carry multiple freights per arc. Having multiple planning entity classes directly raises the implementation complexity of your use case.

Note

Do not create unnecessary planning entity classes. This leads to difficult Move implementations and slower score calculation.

For example, do not create a planning entity class to hold the total free time of a teacher, which needs to be kept up to date as the Lecture planning entities change. Instead, calculate the free time in the score constraints and put the result per teacher into a logically inserted score object.

If historic data needs to be considered too, then create problem fact to hold the total of the historic assignments up to, but not including, the planning window (so it doesn't change when a planning entity changes) and let the score constraints take it into account.

Some optimization algorithms work more efficiently if they have an estimation of which planning entities are more difficult to plan. For example: in bin packing bigger items are harder to fit, in course scheduling lectures with more students are more difficult to schedule and in n queens the middle queens are more difficult to fit on the board.

Therefore, you can set a difficultyComparatorClass to the @PlanningEntity annotation:

@PlanningEntity(difficultyComparatorClass = CloudProcessDifficultyComparator.class)
public class CloudProcess {
    // ...
}
public class CloudProcessDifficultyComparator implements Comparator<CloudProcess> {

    public int compare(CloudProcess a, CloudProcess b) {
        return new CompareToBuilder()
                .append(a.getRequiredMultiplicand(), b.getRequiredMultiplicand())
                .append(a.getId(), b.getId())
                .toComparison();
    }

}

Alternatively, you can also set a difficultyWeightFactoryClass to the @PlanningEntity annotation, so you have access to the rest of the problem facts from the Solution too:

@PlanningEntity(difficultyWeightFactoryClass = QueenDifficultyWeightFactory.class)
public class Queen {
    // ...
}

See sorted selection for more information.

Important

Difficulty should be implemented ascending: easy entities are lower, difficult entities are higher. For example in bin packing: small item < medium item < big item.

Even though some algorithms start with the more difficult entities first, they just reverse the ordering.

None of the current planning variable states should be used to compare planning entity difficult. During Construction Heuristics, those variables are likely to be null anyway. For example, a Queen's row variable should not be used.

A planning variable is a property (including getter and setter) on a planning entity. It points to a planning value, which changes during planning. For example, a Queen's row property is a planning variable. Note that even though a Queen's row property changes to another Row during planning, no Row instance itself is changed.

A planning variable getter needs to be annotated with the @PlanningVariable annotation, which needs a non-empty valueRangeProviderRefs property.

@PlanningEntity
public class Queen {

    private Row row;

    // ...

    @PlanningVariable(valueRangeProviderRefs = {"rowRange"})
    public Row getRow() {
        return row;
    }

    public void setRow(Row row) {
        this.row = row;
    }

}

The valueRangeProviderRefs property defines what are the possible planning values for this planning variable. It references 1 or more @ValueRangeProvider id's.

By default, an initialized planning variable cannot be null, so an initialized solution will never use null for any of its planning variables. In an over-constrained use case, this can be counterproductive. For example: in task assignment with too many tasks for the workforce, we would rather leave low priority tasks unassigned instead of assigning them to an overloaded worker.

To allow an initialized planning variable to be null, set nullable to true:

    @PlanningVariable(..., nullable = true)
    public Worker getWorker() {
        return worker;
    }

Important

Planner will automatically add the value null to the value range. There is no need to add null in a collection used by a ValueRangeProvider.

Note

Using a nullable planning variable implies that your score calculation is responsible for punishing (or even rewarding) variables with a null value.

Repeated planning (especially real-time planning) does not mix well with a nullable planning variable: every time the Solver starts or a problem fact change is made, the Construction Heuristics will try to initialize all the null variables again, which can be a huge waste of time. One way to deal with this, is to change when a planning entity should be reinitialized with an reinitializeVariableEntityFilter:

    @PlanningVariable(..., nullable = true, reinitializeVariableEntityFilter = ReinitializeTaskFilter.class)
    public Worker getWorker() {
        return worker;
    }

A planning variable is considered initialized if its value is not null or if the variable is nullable. So a nullable variable is always considered initialized, even when a custom reinitializeVariableEntityFilter triggers a reinitialization during construction heuristics.

A planning entity is initialized if all of its planning variables are initialized.

A Solution is initialized if all of its planning entities are initialized.

A planning value is a possible value for a planning variable. Usually, a planning value is a problem fact, but it can also be any object, for example a double. It can even be another planning entity or even a interface implemented by both a planning entity and a problem fact.

A planning value range is the set of possible planning values for a planning variable. This set can be a countable (for example row 1, 2, 3 or 4) or uncountable (for example any double between 0.0 and 1.0).

The value range of a planning variable is defined with the @ValueRangeProvider annotation. A @ValueRangeProvider annotation always has a property id, which is referenced by the @PlanningVariable's property valueRangeProviderRefs.

This annotation can be located on 2 types of methods:

The return type of that method can be 2 types:

All instances of the same planning entity class share the same set of possible planning values for that planning variable. This is the most common way to configure a value range.

The Solution implementation has method which returns a Collection (or a ValueRange). Any value from that Collection is a possible planning value for this planning variable.

    @PlanningVariable(valueRangeProviderRefs = {"rowRange"})
    public Row getRow() {
        return row;
    }
@PlanningSolution
public class NQueens implements Solution<SimpleScore> {

    // ...

    @ValueRangeProvider(id = "rowRange")
    public List<Row> getRowList() {
        return rowList;
    }

}

Important

That Collection (or ValueRange) must not contain the value null, not even for a nullable planning variable.

Each planning entity has its own value range (a set of possible planning values) for the planning variable. For example, if a teacher can never teach in a room that does not belong to his department, lectures of that teacher can limit their room value range to the rooms of his department.

    @PlanningVariable(valueRangeProviderRefs = {"departmentRoomRange"})
    public Room getRoom() {
        return room;
    }

    @ValueRangeProvider(id = "departmentRoomRange")
    public List<Room> getPossibleRoomList() {
        return getCourse().getTeacher().getDepartment().getRoomList();
    }

Never use this to enforce a soft constraint (or even a hard constraint when the problem might not have a feasible solution). For example: Unless there is no other way, a teacher can not teach in a room that does not belong to his department. In this case, the teacher should not be limited in his room value range (because sometimes there is no other way).

Note

By limiting the value range specifically of 1 planning entity, you are effectively creating a built-in hard constraint. This can be a very good thing, as the number of possible solutions is severely lowered. But this can also be a bad thing because it takes away the freedom of the optimization algorithms to temporarily break that constraint in order to escape from a local optimum.

A planning entity should not use other planning entities to determinate its value range. That would only try to make it solve the planning problem itself and interfere with the optimization algorithms.

Every entity has its own List instance, except if multiple entity have the same value range. For example, if teacher A and B belong to the same department, they use the same List<Room> instance. Furthermore, each List contains a subset of the same set of planning value instances. For example, if department A and B can both use room X, then their List<Room> instances contain the same Room instance.

Warning

A value range on planning entity is not (yet) compatible with a chained variable.

Instead of a Collection, you can also return a ValueRange or CountableValueRange, build by the ValueRangeFactory:

    @ValueRangeProvider(id = "delayRange")
    public CountableValueRange<Integer> getDelayRange() {
        return ValueRangeFactory.createIntValueRange(0, 5000);
    }

A ValueRange uses far less memory, because it only holds the bounds. In the example above, a Collection would need to hold all 5000 ints, instead of just the 2 bounds.

Furthermore, an incrementUnit can be specified, for example if you have to buy stocks in units of 200 pieces:

    @ValueRangeProvider(id = "stockAmountRange")
    public CountableValueRange<Integer> getStockAmountRange() {
         // Range: 0, 200, 400, 600, ..., 9999600, 9999800, 10000000
        return ValueRangeFactory.createIntValueRange(0, 10000000, 200);
    }

Note

Return CountableValueRange instead of ValueRange whenever possible (so Planner knows it's countable).

The ValueRangeFactory supports several value class types:

Value range providers can be combined, for example:

    @PlanningVariable(valueRangeProviderRefs = {"companyCarRange", "personalCarRange"})
    public Car getCar() {
        return car;
    }
    @ValueRangeProvider(id = "companyCarRange")
    public List<CompanyCar> getCompanyCarList() {
        return companyCarList;
    }

    @ValueRangeProvider(id = "personalCarRange")
    public List<PersonalCar> getPersonalCarList() {
        return personalCarList;
    }

Some optimization algorithms work more efficiently if they have an estimation of which planning values are stronger, which means they are more likely to satisfy a planning entity. For example: in bin packing bigger containers are more likely to fit an item and in course scheduling bigger rooms are less likely to break the student capacity constraint.

Therefore, you can set a strengthComparatorClass to the @PlanningVariable annotation:

    @PlanningVariable(..., strengthComparatorClass = CloudComputerStrengthComparator.class)
    public CloudComputer getComputer() {
        // ...
    }
public class CloudComputerStrengthComparator implements Comparator<CloudComputer> {

    public int compare(CloudComputer a, CloudComputer b) {
        return new CompareToBuilder()
                .append(a.getMultiplicand(), b.getMultiplicand())
                .append(b.getCost(), a.getCost()) // Descending (but this is debatable)
                .append(a.getId(), b.getId())
                .toComparison();
    }

}

Note

If you have multiple planning value classes in the same value range, the strengthComparatorClass needs to implement a Comparator of a common superclass (for example Comparator<Object>) and be able to handle comparing instances of those different classes.

Alternatively, you can also set a strengthWeightFactoryClass to the @PlanningVariable annotation, so you have access to the rest of the problem facts from the solution too:

    @PlanningVariable(..., strengthWeightFactoryClass = RowStrengthWeightFactory.class)
    public Row getRow() {
        // ...
    }

See sorted selection for more information.

Important

Strength should be implemented ascending: weaker values are lower, stronger values are higher. For example in bin packing: small container < medium container < big container.

None of the current planning variable state in any of the planning entities should be used to compare planning values. During construction heuristics, those variables are likely to be null anyway. For example, none of the row variables of any Queen may be used to determine the strength of a Row.

Some use cases, such as TSP and Vehicle Routing, require chaining. This means the planning entities point to each other and form a chain. By modeling the problem as a set of chains (instead of a set of trees/loops), the search space is heavily reduced.

A planning variable that is chained either:

Here are some example of valid and invalid chains:

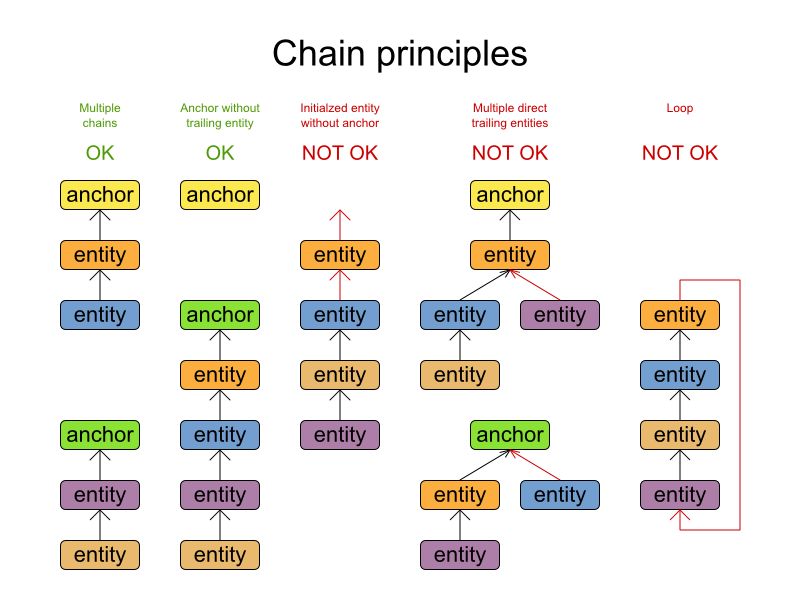
Every initialized planning entity is part of an open-ended chain that begins from an anchor. A valid model means that:

Warning

A planning problem instance given to the Solver must be valid.

Note

If your constraints dictate a closed chain, model it as an open-ended chain (which is easier to persist in a database) and implement a score constraint for the last entity back to the anchor.

The optimization algorithms and built-in Move's do chain correction to guarantee that the model stays valid:

Warning

A custom Move implementation must leave the model in a valid state.

For example, in TSP the anchor is a Domicile (in vehicle routing it is Vehicle):

public class Domicile ... implements Standstill {

    ...

    public City getCity() {...}

}

The anchor (which is a problem fact) and the planning entity implement a common interface, for example TSP's Standstill:

public interface Standstill {

    City getCity();

}

That interface is the return type of the planning variable. Furthermore, the planning variable is chained. For example TSP's Visit (in vehicle routing it is Customer):

@PlanningEntity
public class Visit ... implements Standstill {

    ...

    public City getCity() {...}

    @PlanningVariable(graphType = PlanningVariableGraphType.CHAINED, valueRangeProviderRefs = {"domicileRange", "visitRange"})
    public Standstill getPreviousStandstill() {
        return previousStandstill;
    }

    public void setPreviousStandstill(Standstill previousStandstill) {
        this.previousStandstill = previousStandstill;
    }

}

Notice how 2 value range providers are usually combined:

A shadow variable is a variable whose correct value can be deduced from the state of the genuine planning variables. Even though such a variable violates the principle of normalization by definition, in some use cases it can be very practical to use a shadow variable, especially to express the constraints more naturally. For example in vehicle routing with time windows: the arrival time at a customer for a vehicle can be calculated based on the previously visited customers of that vehicle (and the known travel times between 2 locations).

When the customers for a vehicle change, the arrival time for each customer is automatically adjusted. For more information, see the vehicle routing domain model.

From a score calculation perspective, a shadow variable is like any other planning variable. From an optimization perspective, Planner effectively only optimizes the genuine variables (and mostly ignores the shadow variables): it just assures that when a genuine variable changes, any dependent shadow variables are changed accordingly.

There are several build-in shadow variables:

2 variables are bi-directional if their instances always point to each other (unless they point to null). So if A references B, then B references A.

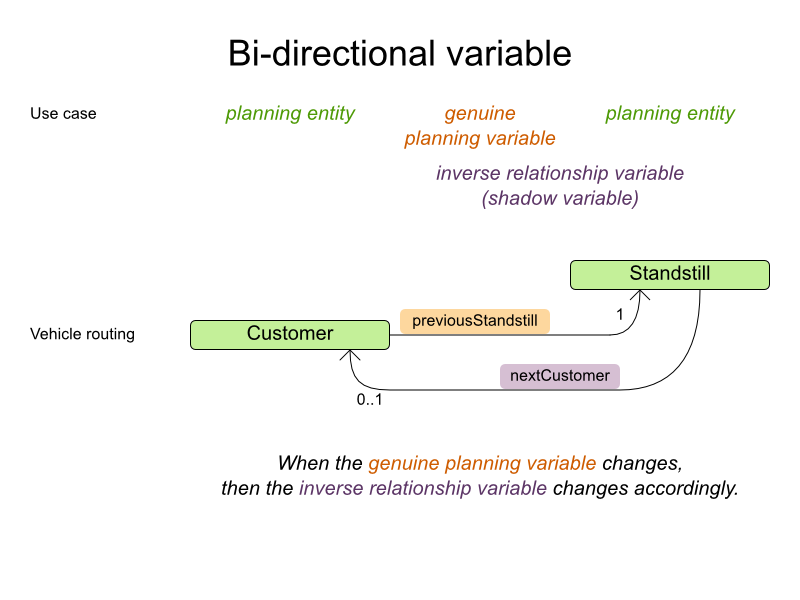
To map a bi-directional relationship between 2 planning variables, annotate the master side as a normal (= genuine) planning variable:

@PlanningEntity
public class Customer ... {

    @PlanningVariable(graphType = PlanningVariableGraphType.CHAINED, ...)
    public Standstill getPreviousStandstill() {
        return previousStandstill;
    }

    public void setPreviousStandstill(Standstill previousStandstill) {...}

}

And then annotate the other side as a @InverseRelationShadowVariable annotation.

@PlanningEntity
public interface Standstill {

    @InverseRelationShadowVariable(sourceVariableName = "previousStandstill")
    Customer getNextCustomer();
    void setNextCustomer(Customer nextCustomer);

}

The sourceVariableName property is the name of the planning variable on the return type of the getter.

Currently, only chained variables support a @InverseRelationShadowVariable annotation.

An anchor shadow variable is the anchor of a chained variable.

Annotate the anchor property as a @AnchorShadowVariable annotation:

@PlanningEntity
public class Customer {

    @AnchorShadowVariable(sourceVariableName = "previousStandstill")
    public Vehicle getVehicle() {...}
    public void setVehicle(Vehicle vehicle) {...}

}

The sourceVariableName property is the name of the chained variable on the same entity class.

To update a shadow variable, Planner uses a VariableListener. To define a custom shadow variable, write a custom VariableListener: implement the interface and annotate it on the shadow variable that needs to change.

    @PlanningVariable(...)
    public Standstill getPreviousStandstill() {
        return previousStandstill;
    }

    @CustomShadowVariable(variableListenerClass = VehicleUpdatingVariableListener.class,
            sources = {@CustomShadowVariable.Source(variableName = "previousStandstill")})
    public Vehicle getVehicle() {
        return vehicle;
    }

The variableName is the variable that triggers changes in the shadow variable(s).

Note

If the class of the trigger variable is different than the shadow variable, also specify the entityClass on @CustomShadowVariable.Source. In that case, make sure that that entityClass is also properly configured as a planning entity class in the solver config, or the VariableListener will simply never trigger.

Any class that has at least 1 shadow variable, is a planning entity class, even it has no genuine planning variables.

For example, the VehicleUpdatingVariableListener assures that every Customer in a chain has the same Vehicle, namely the chain's anchor.

public class VehicleUpdatingVariableListener implements VariableListener<Customer> {

    public void afterEntityAdded(ScoreDirector scoreDirector, Customer customer) {
        updateVehicle(scoreDirector, customer);
    }

    public void afterVariableChanged(ScoreDirector scoreDirector, Customer customer) {
        updateVehicle(scoreDirector, customer);
    }

    ...

    protected void updateVehicle(ScoreDirector scoreDirector, Customer sourceCustomer) {
        Standstill previousStandstill = sourceCustomer.getPreviousStandstill();
        Vehicle vehicle = previousStandstill == null ? null : previousStandstill.getVehicle();
        Customer shadowCustomer = sourceCustomer;
        while (shadowCustomer != null && shadowCustomer.getVehicle() != vehicle) {
            scoreDirector.beforeVariableChanged(shadowCustomer, "vehicle");
            shadowCustomer.setVehicle(vehicle);
            scoreDirector.afterVariableChanged(shadowCustomer, "vehicle");
            shadowCustomer = shadowCustomer.getNextCustomer();
        }
    }

}

Warning

A VariableListener can only change shadow variables. It must never change a genuine planning variable or a problem fact.

Warning

Any change of a shadow variable must be told to the ScoreDirector.

A dataset for a planning problem needs to be wrapped in a class for the Solver to solve. You must implement this class. For example in n queens, this in the NQueens class which contains a Column list, a Row list and a Queen list.

A planning problem is actually a unsolved planning solution or - stated differently - an uninitialized Solution. Therefore, that wrapping class must implement the Solution interface. For example in n queens, that NQueens class implements Solution, yet every Queen in a fresh NQueens class is not yet assigned to a Row (their row property is null). So it's not a feasible solution. It's not even a possible solution. It's an uninitialized solution.

You need to present the problem as a Solution instance to the Solver. So you need to have a class that implements the Solution interface:

public interface Solution<S extends Score> {

    S getScore();
    void setScore(S score);

    Collection<? extends Object> getProblemFacts();

}

For example, an NQueens instance holds a list of all columns, all rows and all Queen instances:

public class NQueens implements Solution<SimpleScore> {

    private int n;

    // Problem facts
    private List<Column> columnList;
    private List<Row> rowList;

    // Planning entities
    private List<Queen> queenList;

    // ...
}

A Solution requires a score property. The score property is null if the Solution is uninitialized or if the score has not yet been (re)calculated. The score property is usually typed to the specific Score implementation you use. For example, NQueens uses a SimpleScore:

public class NQueens implements Solution<SimpleScore> {

    private SimpleScore score;

    public SimpleScore getScore() {
        return score;
    }

    public void setScore(SimpleScore score) {
        this.score = score;
    }

    // ...
}

Most use cases use a HardSoftScore instead:

public class CourseSchedule implements Solution<HardSoftScore> {

    private HardSoftScore score;

    public HardSoftScore getScore() {
        return score;
    }

    public void setScore(HardSoftScore score) {
        this.score = score;
    }

    // ...
}

See the Score calculation section for more information on the Score implementations.

The method is only used if Drools is used for score calculation. Other score directors do not use it.

All objects returned by the getProblemFacts() method will be asserted into the Drools working memory, so the score rules can access them. For example, NQueens just returns all Column and Row instances.

    public Collection<? extends Object> getProblemFacts() {
        List<Object> facts = new ArrayList<Object>();
        facts.addAll(columnList);
        facts.addAll(rowList);
        // Do not add the planning entity's (queenList) because that will be done automatically
        return facts;
    }

All planning entities are automatically inserted into the Drools working memory. Do not add them in the method getProblemFacts().

Note

A common mistake is to use facts.add(...) instead of fact.addAll(...) for a Collection, which leads to score rules failing to match because the elements of that Collection aren't in the Drools working memory.

The getProblemFacts() method is not called much: at most only once per solver phase per solver thread.

A cached problem fact is a problem fact that doesn't exist in the real domain model, but is calculated before the Solver really starts solving. The getProblemFacts() method has the chance to enrich the domain model with such cached problem facts, which can lead to simpler and faster score constraints.

For example in examination, a cached problem fact TopicConflict is created for every 2 Topic's which share at least 1 Student.

    public Collection<? extends Object> getProblemFacts() {
        List<Object> facts = new ArrayList<Object>();
        // ...
        facts.addAll(calculateTopicConflictList());
        // ...
        return facts;
    }

    private List<TopicConflict> calculateTopicConflictList() {
        List<TopicConflict> topicConflictList = new ArrayList<TopicConflict>();
        for (Topic leftTopic : topicList) {
            for (Topic rightTopic : topicList) {
                if (leftTopic.getId() < rightTopic.getId()) {
                    int studentSize = 0;
                    for (Student student : leftTopic.getStudentList()) {
                        if (rightTopic.getStudentList().contains(student)) {
                            studentSize++;
                        }
                    }
                    if (studentSize > 0) {
                        topicConflictList.add(new TopicConflict(leftTopic, rightTopic, studentSize));
                    }
                }
            }
        }
        return topicConflictList;
    }

Any score constraint that needs to check if no 2 exams have a topic which share a student are being scheduled close together (depending on the constraint: at the same time, in a row or in the same day), can simply use the TopicConflict instance as a problem fact, instead of having to combine every 2 Student instances.

Most (if not all) optimization algorithms clone the solution each time they encounter a new best solution (so they can recall it later) or to work with multiple solutions in parallel.

Note

There are many ways to clone, such as a shallow clone, deep clone, ... This context focuses on a planning clone.

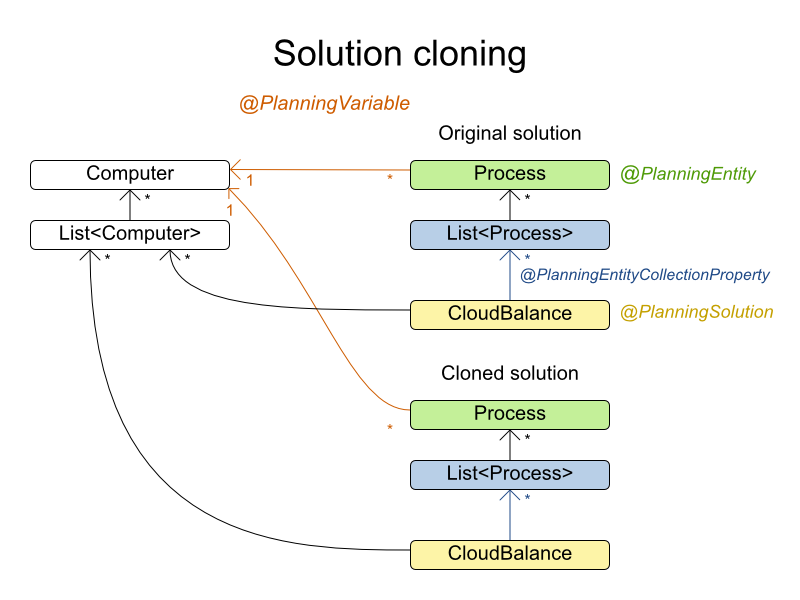
A planning clone of a Solution must fulfill these requirements:

Implementing a planning clone method is hard, therefore you don't need to implement it.

This SolutionCloner is used by default. It works well for most use cases.

Warning

When the FieldAccessingSolutionCloner clones your entity collection, it might not recognize the implementation and replace it with ArrayList, LinkedHashSet or TreeSet (whichever is more applicable). It recognizes most of the common JDK Collection implementations.

The FieldAccessingSolutionCloner does not clone problem facts by default. If any of your problem facts needs to be deep cloned for a planning clone, for example if the problem fact references a planning entity or the planning solution, mark it with a @DeepPlanningClone annotation:

@DeepPlanningClone
public class SeatDesignationDependency {
    private SeatDesignation leftSeatDesignation; // planning entity
    private SeatDesignation rightSeatDesignation; // planning entity
    ...
}

In the example above, because SeatDesignation is a planning entity (which is deep planning cloned automatically), SeatDesignationDependency must be deep planning cloned too.

Alternatively, the @DeepPlanningClone annotation can also be used on a getter method.

If your Solution implements PlanningCloneable, Planner will automatically choose to clone it by calling the planningClone() method.

public interface PlanningCloneable<T> {

    T planningClone();

}

For example: If NQueens implements PlanningCloneable, it would only deep clone all Queen instances. When the original solution is changed during planning, by changing a Queen, the clone stays the same.

public class NQueens implements Solution<...>, PlanningCloneable<NQueens> {
    ...

    /**
     * Clone will only deep copy the {@link #queenList}.
     */
    public NQueens planningClone() {
        NQueens clone = new NQueens();
        clone.id = id;
        clone.n = n;
        clone.columnList = columnList;
        clone.rowList = rowList;
        List<Queen> clonedQueenList = new ArrayList<Queen>(queenList.size());
        for (Queen queen : queenList) {
            clonedQueenList.add(queen.planningClone());
        }
        clone.queenList = clonedQueenList;
        clone.score = score;
        return clone;
    }
}

The planningClone() method should only deep clone the planning entities. Notice that the problem facts, such as Column and Row are normally not cloned: even their List instances are not cloned. If you were to clone the problem facts too, then you'd have to make sure that the new planning entity clones also refer to the new problem facts clones used by the solution. For example, if you would clone all Row instances, then each Queen clone and the NQueens clone itself should refer to those new Row clones.

Warning

Cloning an entity with a chained variable is devious: a variable of an entity A might point to another entity B. If A is cloned, then it's variable must point to the clone of B, not the original B.

Create a Solution instance to represent your planning problem's dataset, so it can be set on the Solver as the planning problem to solve. For example in n queens, an NQueens instance is created with the required Column and Row instances and every Queen set to a different column and every row set to null.

    private NQueens createNQueens(int n) {
        NQueens nQueens = new NQueens();
        nQueens.setId(0L);
        nQueens.setN(n);
        nQueens.setColumnList(createColumnList(nQueens));
        nQueens.setRowList(createRowList(nQueens));
        nQueens.setQueenList(createQueenList(nQueens));
        return nQueens;
    }

    private List<Queen> createQueenList(NQueens nQueens) {
        int n = nQueens.getN();
        List<Queen> queenList = new ArrayList<Queen>(n);
        long id = 0;
        for (Column column : nQueens.getColumnList()) {
            Queen queen = new Queen();
            queen.setId(id);
            id++;
            queen.setColumn(column);
            // Notice that we leave the PlanningVariable properties on null
            queenList.add(queen);
        }
        return queenList;
    }

Figure 4.1. Uninitialized solution for the 4 queens puzzle

Uninitialized solution for the 4 queens puzzle

Usually, most of this data comes from your data layer, and your Solution implementation just aggregates that data and creates the uninitialized planning entity instances to plan:

        private void createLectureList(CourseSchedule schedule) {
            List<Course> courseList = schedule.getCourseList();
            List<Lecture> lectureList = new ArrayList<Lecture>(courseList.size());
            for (Course course : courseList) {
                for (int i = 0; i < course.getLectureSize(); i++) {
                    Lecture lecture = new Lecture();
                    lecture.setCourse(course);
                    lecture.setLectureIndexInCourse(i);
                    // Notice that we leave the PlanningVariable properties (period and room) on null
                    lectureList.add(lecture);
                }
            }
            schedule.setLectureList(lectureList);
        }

4.4. Use the Solver

A Solver implementation will solve your planning problem.

public interface Solver {
    
    void solve(Solution planningProblem);

    Solution getBestSolution();

    // ...

}

A Solver can only solve 1 planning problem instance at a time. A Solver should only be accessed from a single thread, except for the methods that are specifically javadocced as being thread-safe. It's built with a SolverFactory, do not implement or build it yourself.

Solving a problem is quite easy once you have:

Just set the planning problem, solve it and extract the best solution:

    solver.solve(planningProblem);
    Solution bestSolution = solver.getBestSolution();

For example in n queens, the getBestSolution() method will return an NQueens instance with every Queen assigned to a Row.

Figure 4.2. Best solution for the 4 queens puzzle in 8 ms (also an optimal solution)

Best solution for the 4 queens puzzle in 8 ms (also an optimal solution)

The solve(Solution) method can take a long time (depending on the problem size and the solver configuration). The Solver will remember (actually clone) the best solution it encounters during its solving. Depending on a number factors (including problem size, how much time the Solver has, the solver configuration, ...), that best solution will be a feasible or even an optimal solution.

Note

The Solution instance given to the method solve(Solution) will be changed by the Solver, but do not mistake it for the best solution.

The Solution instance returned by the getBestSolution() method will most likely be a clone of the instance given to the method solve(Solution), which means it's a different instance.

Note

The Solution instance given to the solve(Solution) method does not need to be uninitialized. It can be partially or fully initialized, which is likely to be the case in repeated planning.

The environment mode allows you to detect common bugs in your implementation. It does not affect the logging level.

You can set the environment mode in the solver configuration XML file:

<solver>
  <environmentMode>FAST_ASSERT</environmentMode>
  ...
</solver>

A solver has a single Random instance. Some solver configurations use the Random instance a lot more than others. For example Simulated Annealing depends highly on random numbers, while Tabu Search only depends on it to deal with score ties. The environment mode influences the seed of that Random instance.

These are the environment modes:

The FULL_ASSERT mode turns on all assertions (such as assert that the incremental score calculation is uncorrupted for each move) to fail-fast on a bug in a Move implementation, a score rule, the rule engine itself, ...

This mode is reproducible (see the reproducible mode). It is also intrusive because it calls the method calculateScore() more frequently than a non assert mode.

The FULL_ASSERT mode is horribly slow (because it doesn't rely on incremental score calculation).

The NON_INTRUSIVE_FULL_ASSERT turns on several assertions to fail-fast on a bug in a Move implementation, a score rule, the rule engine itself, ...

This mode is reproducible (see the reproducible mode). It is non-intrusive because it does not call the method calculateScore() more frequently than a non assert mode.

The NON_INTRUSIVE_FULL_ASSERT mode is horribly slow (because it doesn't rely on incremental score calculation).

The FAST_ASSERT mode turns on most assertions (such as assert that an undoMove's score is the same as before the Move) to fail-fast on a bug in a Move implementation, a score rule, the rule engine itself, ...

This mode is reproducible (see the reproducible mode). It is also intrusive because it calls the method calculateScore() more frequently than a non assert mode.

The FAST_ASSERT mode is slow.

It's recommended to write a test case which does a short run of your planning problem with the FAST_ASSERT mode on.

The reproducible mode is the default mode because it is recommended during development. In this mode, 2 runs in the same Planner version will execute the same code in the same order. Those 2 runs will have the same result at every step, except if the note below applies. This enables you to reproduce bugs consistently. It also allows you to benchmark certain refactorings (such as a score constraint performance optimization) fairly across runs.

Note

Despite the reproducible mode, your application might still not be fully reproducible because of:

The reproducible mode is slightly slower than the production mode. If your production environment requires reproducibility, use this mode in production too.

In practice, this mode uses the default, fixed random seed if no seed is specified, and it also disables certain concurrency optimizations (such as work stealing).

The production mode is the fastest, but it is not reproducible. It is recommended for a production environment, unless reproducibility is required.

In practice, this mode uses no fixed random seed if no seed is specified.

The best way to illuminate the black box that is a Solver, is to play with the logging level:

For example, set it to debug logging, to see when the phases end and how fast steps are taken:

INFO  Solving started: time spent (3), best score (uninitialized/0), random (JDK with seed 0).
DEBUG     CH step (0), time spent (5), score (0), selected move count (1), picked move (col2@null => row0).
DEBUG     CH step (1), time spent (7), score (0), selected move count (3), picked move (col1@null => row2).
DEBUG     CH step (2), time spent (10), score (0), selected move count (4), picked move (col3@null => row3).
DEBUG     CH step (3), time spent (12), score (-1), selected move count (4), picked move (col0@null => row1).
INFO  Construction Heuristic phase (0) ended: step total (4), time spent (12), best score (-1).
DEBUG     LS step (0), time spent (19), score (-1),     best score (-1), accepted/selected move count (12/12), picked move (col1@row2 => row3).
DEBUG     LS step (1), time spent (24), score (0), new best score (0), accepted/selected move count (9/12), picked move (col3@row3 => row2).
INFO  Local Search phase (1) ended: step total (2), time spent (24), best score (0).
INFO  Solving ended: time spent (24), best score (0), average calculate count per second (1625).

All time spent values are in milliseconds.

Everything is logged to SLF4J, which is a simple logging facade which delegates every log message to Logback, Apache Commons Logging, Log4j or java.util.logging. Add a dependency to the logging adaptor for your logging framework of choice.

If you're not using any logging framework yet, use Logback by adding this Maven dependency (there is no need to add an extra bridge dependency):

    <dependency>
      <groupId>ch.qos.logback</groupId>
      <artifactId>logback-classic</artifactId>
      <version>1.x</version>
    </dependency>

Configure the logging level on the org.optaplanner package in your logback.xml file:

<configuration>

  <logger name="org.optaplanner" level="debug"/>

  ...

<configuration>

If instead, you're still using Log4J 1.x (and you don't want to switch to its faster successor, Logback), add the bridge dependency:

    <dependency>
      <groupId>org.slf4j</groupId>
      <artifactId>slf4j-log4j12</artifactId>
      <version>1.x</version>
    </dependency>

And configure the logging level on the package org.optaplanner in your log4j.xml file:

<log4j:configuration xmlns:log4j="http://jakarta.apache.org/log4j/">

  <category name="org.optaplanner">
    <priority value="debug" />
  </category>

  ...

</log4j:configuration>

Note

In a multitenant application, multiple Solver instances might be running at the same time. To separate their logging into distinct files, surround the solve() call with an MDC:

        MDC.put("tenant.name",tenantName);
        solver.solve(planningProblem);
        Solution bestSolution = solver.getBestSolution();
        MDC.remove("tenant.name");

Then configure your logger to use different files for each ${tenant.name}. For example in Logback, use a SiftingAppender in logback.xml:

  <appender name="fileAppender" class="ch.qos.logback.classic.sift.SiftingAppender">
    <discriminator>
      <key>tenant.name</key>
      <defaultValue>unknown</defaultValue>
    </discriminator>
    <sift>
      <appender name="fileAppender.${tenant.name}" class="...FileAppender">
        <file>local/log/optaplanner-${tenant.name}.log</file>
        ...
      </appender>
    </sift>
  </appender>

Many heuristics and metaheuristics depend on a pseudorandom number generator for move selection, to resolve score ties, probability based move acceptance, ... During solving, the same Random instance is reused to improve reproducibility, performance and uniform distribution of random values.

To change the random seed of that Random instance, specify a randomSeed:

<solver>
  <randomSeed>0</randomSeed>
  ...
</solver>

To change the pseudorandom number generator implementation, specify a randomType:

<solver>
  <randomType>MERSENNE_TWISTER</randomType>
  ...
</solver>

The following types are supported:

For most use cases, the randomType has no significant impact on the average quality of the best solution on multiple datasets. If you want to confirm this on your use case, use the benchmarker.