Every initialized Solution has a score. The score is an objective way to compare two solutions. The solution with the higher score is better. The Solver aims to find the Solution with the highest Score of all possible solutions. The best solution is the Solution with the highest Score that Solver has encountered during solving, which might be the optimal solution.

Planner cannot automatically know which Solution is best for your business, so you need to tell it how to calculate the score of a given Solution according to your business needs. If you forget or are unable to implement an important business constraint, the solution is probably useless:

Defining constraints in Planner is very flexible through the following score techniques:

All score techniques are based on constraints. A constraint can be a simple pattern (such as Maximize the apple harvest in the solution) or a more complex pattern. A positive constraint is a constraint you want to maximize. A negative constraint is a constraint you want to minimize.

The image above illustrates that the optimal solution always has the highest score, regardless if the constraints are positive or negative.

Most planning problems have only negative constraints and therefore have a negative score. In that case, the score is the sum of the weight of the negative constraints being broken, with a perfect score of 0. This explains why the score of a solution of four queens is the negative of the number of queen pairs which can attack each other.

Negative and positive constraints can be combined, even in the same score level.

When a constraint activates (because the negative constraint is broken or the positive constraint is fulfilled) on a certain planning entity set, it is called a constraint match.

Not all score constraints are equally important. If breaking one constraint is equally bad as breaking another constraint x times, then those two constraints have a different weight (but they are in the same score level). For example in vehicle routing, you can make one "unhappy driver" constraint match count as much as two "fuel tank usage" constraint matches:

Score weighting is often used in use cases where you can put a price tag on everything. In that case, the positive constraints maximize revenue and the negative constraints minimize expenses, so together they maximize profit. Alternatively, score weighting is also often used to create social fairness. For example, a nurse, who requests a free day, pays a higher weight on New Years eve than on a normal day.

Putting a good weight on a constraint can be a difficult analytical decision, because it is about making choices and tradeoffs with other constraints. However, a non-accurate weight is less damaging than mediocre algorithms:

The weight of a constraint match can be dynamically based on the planning entities involved. For example in cloud balance, the weight of the soft constraint match for an active Computer is the cost of that Computer (which differs per computer).

Sometimes a score constraint outranks another score constraint, no matter how many times the other is broken. In that case, those score constraints are in different levels. For example, a nurse cannot do 2 shifts at the same time (due to the constraints of physical reality), this outranks all nurse happiness constraints.

Most use cases have only two score levels, hard and soft. Two scores are compared lexicographically. The first score level gets compared first. If those differ, the others score levels are ignored. For example, a score that breaks 0 hard constraints and 1000000 soft constraints is better than a score that breaks 1 hard constraint and 0 soft constraints.

If there are two (or more) score levels, for example a hard and soft level, then a score is feasible if no hard constraints are broken.

For each constraint, you need to pick a score level, a score weight and a score signum. For example: -1soft which has score level of soft, a weight of 1 and a negative signum. Do not use a big constraint weight when your business actually wants different score levels. That hack, known as score folding, is broken:

Three or more score levels are supported. For example: a company might decide that profit outranks employee satisfaction (or visa versa), while both are outranked by the constraints of physical reality.

Far less common is the use case of pareto optimization, which is also known under the more confusing term multi-objective optimization. In pareto scoring, score constraints are in the same score level, yet they are not weighted against each other. When two scores are compared, each of the score constraints are compared individually and the score with the most dominating score constraints wins. Pareto scoring can even be combined with score levels and score constraint weighting.

Consider this example with positive constraints, where we want to get the most apples and oranges. Since it is impossible to compare apples and oranges, we can not weight them against each other. Yet, despite that we can not compare them, we can state that two apples are better then one apple. Similarly, we can state that two apples and one orange are better than just one orange. So despite our inability to compare some Scores conclusively (at which point we declare them equal), we can find a set of optimal scores. Those are called pareto optimal.

Scores are considered equal far more often. It is left up to a human to choose the better out of a set of best solutions (with equal scores) found by Planner. In the example above, the user must choose between solution A (three apples and one orange) and solution B (one apple and six oranges). It is guaranteed that Planner has not found another solution which has more apples or more oranges or even a better combination of both (such as two apples and three oranges).

To implement pareto scoring in Planner, implement a custom ScoreDefinition and Score (and replace the BestSolutionRecaller). Future versions will provide out-of-the-box support.

All the score techniques mentioned above, can be combined seamlessly:

A score is represented by the Score interface, which naturally extends Comparable:

public interface Score<...> extends Comparable<...> {
    ...
}

The Score implementation to use depends on your use case. Your score might not efficiently fit in a single long value. Planner has several built-in Score implementations, but you can implement a custom Score too. Most use cases tend to use the built-in HardSoftScore.

The Score implementation (for example HardSoftScore) must be the same throughout a Solver runtime. The Score implementation is configured in the solver configuration as a ScoreDefinition:

  <scoreDirectorFactory>
    <scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
    ...
  </scoreDirectorFactory>

Avoid the use of float and double for score calculation. Use BigDecimal instead.

Floating point numbers (float and double) cannot represent a decimal number correctly. For example: a double cannot hold the value 0.05 correctly. Instead, it holds the nearest representable value. Arithmetic (including addition and subtraction) with floating point numbers, especially for planning problems, leads to incorrect decisions:

Additionally, floating point number addition is not associative:

System.out.println( ((0.01 + 0.02) + 0.03) == (0.01 + (0.02 + 0.03)) ); // returns false

This leads to score corruption.

Decimal numbers (BigDecimal) have none of these problems.

A SimpleScore has a single int value, for example -123. It has a single score level.

  <scoreDirectorFactory>
    <scoreDefinitionType>SIMPLE</scoreDefinitionType>
    ...
  </scoreDirectorFactory>

Variants of this scoreDefinitionType:

A HardSoftScore has a hard int value and a soft int value, for example -123hard/-456soft. It has 2 score levels (hard and soft).

  <scoreDirectorFactory>
    <scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
    ...
  </scoreDirectorFactory>

Variants of this scoreDefinitionType:

A HardMediumSoftScore which has a hard int value, a medium int value and a soft int value, for example -123hard/-456medium/-789soft. It has 3 score levels (hard, medium and soft).

  <scoreDirectorFactory>
    <scoreDefinitionType>HARD_MEDIUM_SOFT</scoreDefinitionType>
    ...
  </scoreDirectorFactory>

Variants of this scoreDefinitionType:

A BendableScore has a configurable number of score levels. It has an array of hard int values and an array of soft int value, for example with 2 hard levels and 3 soft levels, the score can be -123/-456/-789/-012/-345.

  <scoreDirectorFactory>
    <scoreDefinitionType>BENDABLE</scoreDefinitionType>
    <bendableHardLevelsSize>2</bendableHardLevelsSize>
    <bendableSoftLevelsSize>3</bendableSoftLevelsSize>
    ...
  </scoreDirectorFactory>

The number of hard and soft score levels needs to be set at configuration time. It is not flexible to change during solving.

Variants of this scoreDefinitionType:

The ScoreDefinition interface defines the score representation.

To implement a custom Score, you will also need to implement a custom ScoreDefinition. Extend AbstractScoreDefinition (preferably by copy pasting HardSoftScoreDefinition) and start from there.

Then hook your custom ScoreDefinition in your SolverConfig.xml:

  <scoreDirectorFactory>
    <scoreDefinitionClass>...MyScoreDefinition</scoreDefinitionClass>
    ...
  </scoreDirectorFactory>

To have it integrate seamlessly with JPA/Hibernate, XStream, ... you might need to write some glue code.

There are several ways to calculate the Score of a Solution:

Every score calculation type can use any Score definition. For example, easy Java score calculation can output a HardSoftScore.

All score calculation types are Object Oriented and can reuse existing Java code.

An easy way to implement your score calculation in Java.

Just implement one method of the interface EasyScoreCalculator:

public interface EasyScoreCalculator<Sol extends Solution> {

    Score calculateScore(Sol solution);
   
}

For example in n queens:

public class NQueensEasyScoreCalculator implements EasyScoreCalculator<NQueens> {

    public SimpleScore calculateScore(NQueens nQueens) {
        int n = nQueens.getN();
        List<Queen> queenList = nQueens.getQueenList();
        
        int score = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                Queen leftQueen = queenList.get(i);
                Queen rightQueen = queenList.get(j);
                if (leftQueen.getRow() != null && rightQueen.getRow() != null) {
                    if (leftQueen.getRowIndex() == rightQueen.getRowIndex()) {
                        score--;
                    }
                    if (leftQueen.getAscendingDiagonalIndex() == rightQueen.getAscendingDiagonalIndex()) {
                        score--;
                    }
                    if (leftQueen.getDescendingDiagonalIndex() == rightQueen.getDescendingDiagonalIndex()) {
                        score--;
                    }
                }
            }
        }
        return SimpleScore.valueOf(score);
    }

}

Configure it in your solver configuration:

  <scoreDirectorFactory>
    <scoreDefinitionType>...</scoreDefinitionType>
    <easyScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensEasyScoreCalculator</easyScoreCalculatorClass>
  </scoreDirectorFactory>

Alternatively, build a EasyScoreCalculator instance at runtime and set it with the programmatic API:

    solverFactory.getSolverConfig().getScoreDirectorFactoryConfig.setEasyScoreCalculator(easyScoreCalculator);

A way to implement your score calculation incrementally in Java.

Implement all the methods of the interface IncrementalScoreCalculator and extend the class AbstractIncrementalScoreCalculator:

public interface IncrementalScoreCalculator<Sol extends Solution> {

    void resetWorkingSolution(Sol workingSolution);

    void beforeEntityAdded(Object entity);

    void afterEntityAdded(Object entity);

    void beforeVariableChanged(Object entity, String variableName);

    void afterVariableChanged(Object entity, String variableName);

    void beforeEntityRemoved(Object entity);

    void afterEntityRemoved(Object entity);

    Score calculateScore();
    
}

For example in n queens:

public class NQueensAdvancedIncrementalScoreCalculator extends AbstractIncrementalScoreCalculator<NQueens> {

    private Map<Integer, List<Queen>> rowIndexMap;
    private Map<Integer, List<Queen>> ascendingDiagonalIndexMap;
    private Map<Integer, List<Queen>> descendingDiagonalIndexMap;

    private int score;

    public void resetWorkingSolution(NQueens nQueens) {
        int n = nQueens.getN();
        rowIndexMap = new HashMap<Integer, List<Queen>>(n);
        ascendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
        descendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
        for (int i = 0; i < n; i++) {
            rowIndexMap.put(i, new ArrayList<Queen>(n));
            ascendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
            descendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
            if (i != 0) {
                ascendingDiagonalIndexMap.put(n - 1 + i, new ArrayList<Queen>(n));
                descendingDiagonalIndexMap.put((-i), new ArrayList<Queen>(n));
            }
        }
        score = 0;
        for (Queen queen : nQueens.getQueenList()) {
            insert(queen);
        }
    }

    public void beforeEntityAdded(Object entity) {
        // Do nothing
    }

    public void afterEntityAdded(Object entity) {
        insert((Queen) entity);
    }

    public void beforeVariableChanged(Object entity, String variableName) {
        retract((Queen) entity);
    }

    public void afterVariableChanged(Object entity, String variableName) {
        insert((Queen) entity);
    }

    public void beforeEntityRemoved(Object entity) {
        retract((Queen) entity);
    }

    public void afterEntityRemoved(Object entity) {
        // Do nothing
    }

    private void insert(Queen queen) {
        Row row = queen.getRow();
        if (row != null) {
            int rowIndex = queen.getRowIndex();
            List<Queen> rowIndexList = rowIndexMap.get(rowIndex);
            score -= rowIndexList.size();
            rowIndexList.add(queen);
            List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
            score -= ascendingDiagonalIndexList.size();
            ascendingDiagonalIndexList.add(queen);
            List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
            score -= descendingDiagonalIndexList.size();
            descendingDiagonalIndexList.add(queen);
        }
    }

    private void retract(Queen queen) {
        Row row = queen.getRow();
        if (row != null) {
            List<Queen> rowIndexList = rowIndexMap.get(queen.getRowIndex());
            rowIndexList.remove(queen);
            score += rowIndexList.size();
            List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
            ascendingDiagonalIndexList.remove(queen);
            score += ascendingDiagonalIndexList.size();
            List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
            descendingDiagonalIndexList.remove(queen);
            score += descendingDiagonalIndexList.size();
        }
    }

    public SimpleScore calculateScore() {
        return SimpleScore.valueOf(score);
    }

}

Configure it in your solver configuration:

  <scoreDirectorFactory>
    <scoreDefinitionType>...</scoreDefinitionType>
    <incrementalScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensAdvancedIncrementalScoreCalculator</incrementalScoreCalculatorClass>
  </scoreDirectorFactory>

Optionally, to explain a score with ScoreDirector.getConstraintMatchTotals() or to get better output when the IncrementalScoreCalculator is corrupted in FAST_ASSERT or FULL_ASSERT environmentMode, implement also the ConstraintMatchAwareIncrementalScoreCalculator interface:

public interface ConstraintMatchAwareIncrementalScoreCalculator<Sol extends Solution> {

    void resetWorkingSolution(Sol workingSolution, boolean constraintMatchEnabled);

    Collection<ConstraintMatchTotal> getConstraintMatchTotals();
    
}

The InitializingScoreTrend specifies how the Score will change as more and more variables are initialized (while the already initialized variables do not change). Some optimization algorithms (such Construction Heuristics and Exhaustive Search) run faster if they have such information.

For for the Score (or each score level separately), specify a trend:

Most use cases only have negative constraints. Many of those have an InitializingScoreTrend that only goes down:

  <scoreDirectorFactory>
    <scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
    <scoreDrl>.../cloudBalancingScoreRules.drl</scoreDrl>
    <initializingScoreTrend>ONLY_DOWN</initializingScoreTrend>
  </scoreDirectorFactory>

Alternatively, you can also specify the trend for each score level separately:

  <scoreDirectorFactory>
    <scoreDefinitionType>HARD_SOFT</scoreDefinitionType>
    <scoreDrl>.../cloudBalancingScoreRules.drl</scoreDrl>
    <initializingScoreTrend>ONLY_DOWN/ONLY_DOWN</initializingScoreTrend>
  </scoreDirectorFactory>

Put the environmentMode in FULL_ASSERT (or FAST_ASSERT) to detect corruption in the incremental score calculation. For more information, see the section about environmentMode. However, that will not verify that your score calculator implements your score constraints as your business actually desires.

A piece of incremental score calculator code can be difficult to write and to review. Assert its correctness by using a different implementation (for example a EasyScoreCalculator) to do the assertions triggered by the environmentMode. Just configure the different implementation as a assertionScoreDirectorFactory:

  <environmentMode>FAST_ASSERT</environmentMode>
  ...
  <scoreDirectorFactory>
    <scoreDefinitionType>...</scoreDefinitionType>
    <scoreDrl>org/optaplanner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>
    <assertionScoreDirectorFactory>
      <easyScoreCalculatorClass>org.optaplanner.examples.nqueens.solver.score.NQueensEasyScoreCalculator</easyScoreCalculatorClass>
    </assertionScoreDirectorFactory>
  </scoreDirectorFactory>

This way, the scoreDrl will be validated by the EasyScoreCalculator.

The Solver will normally spend most of its execution time running the score calculation (which is called in its deepest loops). Faster score calculation will return the same solution in less time with the same algorithm, which normally means a better solution in equal time.

After solving a problem, the Solver will log the average calculation count per second. This is a good measurement of Score calculation performance, despite that it is affected by non score calculation execution time. It depends on the problem scale of the problem dataset. Normally, even for high scale problems, it is higher than 1000, except when you are using EasyScoreCalculator.

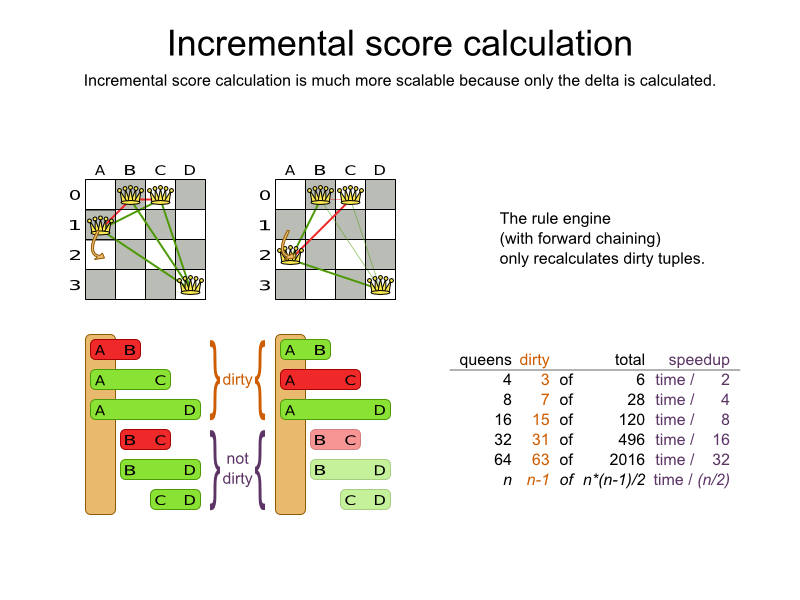
When a Solution changes, incremental score calculation (AKA delta based score calculation), will calculate the delta with the previous state to find the new Score, instead of recalculating the entire score on every solution evaluation.

For example, if a single queen A moves from row 1 to 2, it will not bother to check if queen B and C can attack each other, since neither of them changed.

Figure 5.1. Incremental Score Calculation for the 4 Queens Puzzle

Do not call remote services in your score calculation (except if you are bridging EasyScoreCalculator to a legacy system). The network latency will kill your score calculation performance. Cache the results of those remote services if possible.

If some parts of a constraint can be calculated once, when the Solver starts, and never change during solving, then turn them into cached problem facts.

If you know a certain constraint can never be broken (or it is always broken), you need not write a score constraint for it. For example in n queens, the score calculation does not check if multiple queens occupy the same column, because a Queen's column never changes and every Solution starts with each Queen on a different column.

Instead of implementing a hard constraint, it can sometimes be built in. For example, If Lecture A should never be assigned to Room X, but it uses ValueRangeProvider on Solution, so the Solver will often try to assign it to Room X too (only to find out that it breaks a hard constraint). Use a ValueRangeProvider on the planning entity or filtered selection to define that Course A should only be assigned a Room different than X.

This can give a good performance gain in some use cases, not just because the score calculation is faster, but mainly because most optimization algorithms will spend less time evaluating unfeasible solutions. However, usually this not a good idea because there is a real risk of trading short term benefits for long term harm:

Make sure that none of your score constraints cause a score trap. A trapped score constraint uses the same weight for different constraint matches, when it could just as easily use a different weight. It effectively lumps its constraint matches together, which creates a flatlined score function for that constraint. This can cause a solution state in which several moves need to be done to resolve or lower the weight of that single constraint. Some examples of score traps:

For example, consider this score trap. If the blue item moves from an overloaded computer to an empty computer, the hard score should improve. The trapped score implementation fails to do that:

The Solver should eventually get out of this trap, but it will take a lot of effort (especially if there are even more processes on the overloaded computer). Before they do that, they might actually start moving more processes into that overloaded computer, as there is no penalty for doing so.

There are several ways to deal with a score trap:

Not all score constraints have the same performance cost. Sometimes one score constraint can kill the score calculation performance outright. Use the Benchmarker to do a one minute run and check what happens to the average calculation count per second if you comment out all but one of the score constraints.

Some use cases have a business requirement to provide a fair schedule (usually as a soft score constraint), for example:

Implementing such a constraint can seem difficult (especially because there are different ways to formalize fairness), but usually the squared workload implementation behaves most desirable. For each employee/asset, count the workload w and subtract w² from the score.

As shown above, the squared workload implementation guarantees that if you select two employees from a given solution and make their distribution between those two employees fairer, then the resulting new solution will have a better overall score. Don not just use the difference from the average workload, as that can lead to unfairness, as demonstrated below.

When the workload is perfect balanced, the user often likes to see a 0 score, instead of the distracting -34soft in the image above (for the last solution which is almost perfectly balanced). To nullify this, either add the average multiplied by the number of entities to the score or instead show the variance or standard deviation in the UI.